Artificial Intelligence in Finance, Volume 2: Reinforcement Learning Theory and Practice
First published:
ISBN: 9781782724544
If you are a Risk.net subscriber you are entitled to 20% off your Risk books purchases. Please email enquiries@riskbooks.com for more information.
As part of your Risk.net subscription you are entitled to 20% off all of your Risk Books purchases. If you would like to place an order please email enquiries@riskbooks.com
Pricing options with temporal difference backpropagation
Miquel Noguer i Alonso, Daniel Bloch and David Pacheco Aznar
Preface
Introduction
Markov decision problems
Learning the optimal policy
Reinforcement learning revisited
Temporal difference learning revisited
Stochastic approximation in Markov decision processes
Large language models: reasoning and reinforcement learning
Deep reinforcement learning
Applications of artificial intelligence in finance
Pricing options with temporal difference backpropagation
Pricing American options
Daily price limits
Portfolio optimisation
Appendix
10.1 INTRODUCTION
Quantitative trading and risk management require the computation of expectations. However, we need to recompute the risk–return profile as it evolves over time. Hence, we must dynamically modify our positions based on the surrounding environment and hedge against adverse moves. The problem is that conditional expectations are very difficult to estimate from experiments directly (see Figure 10.1).
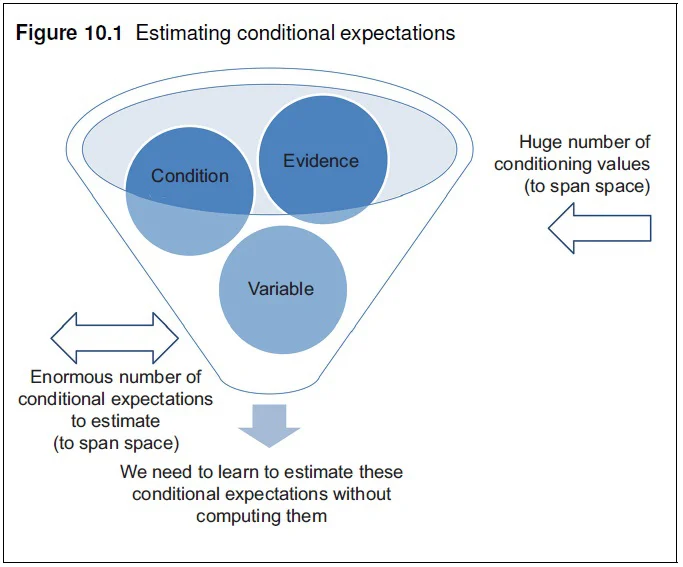
Existing solutions include the following.
-
Parametric models: conditional expectations of path-dependent events are tied to their ability to capture the dynamics of the underlying stochastic processes.
-
Neural networks: these use data to estimate the implicit stochastic processes driving the dynamics of the future events, although they cannot solve multi-step prediction problems.
-
Reinforcement learning: this allows for computations of path dependent payouts from past data; the temporal difference backpropagation (TDBP) model is a special case (see Section 5.6).
There are wide range of numerical techniques for computing conditional expectations (eg, integration, partial differential equations (PDEs), Monte Carlo simulation and Fourier transform)
Copyright Infopro Digital Limited. All rights reserved.
As outlined in our terms and conditions, https://www.infopro-digital.com/terms-and-conditions/subscriptions/ (point 2.4), printing is limited to a single copy.
If you would like to purchase additional rights please email info@risk.net
Copyright Infopro Digital Limited. All rights reserved.
You may share this content using our article tools. As outlined in our terms and conditions, https://www.infopro-digital.com/terms-and-conditions/subscriptions/ (clause 2.4), an Authorised User may only make one copy of the materials for their own personal use. You must also comply with the restrictions in clause 2.5.
If you would like to purchase additional rights please email info@risk.net
