Calibrating interest rate curves for a new era

Dmitry Pugachevsky, director of research at Quantifi, explores why building an accurate and robust interest rate curve has considerable implications for a broad range of financial operations – from setting benchmark rates to managing risk – and hinges on the use of liquid market instruments. These instruments, which include interest rate swaps, futures and government bonds, provide insight into market expectations for future rates to ensure accurate pricing. High trading volumes make these instruments less vulnerable to manipulation, resulting in reliable, anomaly-resistant interest rate curves that reflect actual market conditions
 

Dmitry Pugachevsky, Quantifi

Single-curve bootstrap versus global optimisation

Prior to the financial crisis that began in 2007–08, interest rate curve building followed a relatively straightforward process. However, the financial crisis reshaped market dynamics. The once negligible Libor overnight indexed swap (OIS) spread widened and became volatile. This led to the adoption of dual curve discounting, using Libor for forward rate projection and OIS for discounting.

As the paradigm shifted, a simultaneous solver for both curves became necessary, intensifying the complexity of the problem. The challenge arises from a circular dependency between the curves, where instruments on one curve need information from the other for pricing. This is because various combinations of projection expectations and discount factors can yield the same arbitrage-free rate, requiring simultaneous estimation for realistic results. This entanglement rules out sequential curve construction, necessitating initial disentanglement or a global optimiser.

Despite the phasing out of Libor, diverse traded interest rates are referenced in derivatives and securities. The complexity of accurately constructing risk-free rate (RFR) benchmarks – such as the secured overnight financing rate (SOFR) and US Federal Reserve funds – often demands a global optimisation approach. In some markets – such as Australian interest rates with four interconnected benchmark curves – disentanglement isn’t feasible. These markets have required global optimisation for years and will probably continue to do so.

Global optimisation can outperform bootstrapping when constructing a single curve, especially with advanced interpolation methods such as spline interpolation. This method operates worldwide across the entire curve, requiring multidimensional solving, underscoring the need for global optimisation. In the past decade, significant research has focused on enhancing the stability and performance of these global optimisation algorithms.
 

Entangled curves 

Constructing interdependent or ‘entangled’ curves is a challenge in quantitative finance. Using a multidimensional optimiser can often be slow and unstable. This has prompted researchers and practitioners to seek alternative methods to sidestep the need for a global optimiser while ensuring accurate and reliable results.

An alternative method focuses on addressing cyclical dependencies – primarily through interest rate swaps and, in particular, basis swaps. In certain conditions, it is possible to construct synthetic fixed-to-floating swaps that replicate market data in basis swaps. For instance, a 10-year fixed-to-float swap for an interbank offered rate (Ibor) and a 10-year basis swap between Ibor and OIS rates can be combined to create a synthetic 10-year OIS fixed-to-floating swap. This simplifies the entangled curve challenge into a single curve bootstrap problem.

However, this approach has limitations. The required market instruments may not always be sufficiently liquid. Liquidity varies across markets and time periods. Thus, performant global optimisations are essential in some markets. Quantifi has demonstrated it is possible to implement stable and fast global optimisation algorithms, addressing performance issues.
 

Calibrating SOFR curves

Following the discontinuation of Libor in June 2023, attention shifted to US dollar SOFR and other global RFRs. Daily SOFR rates are now central in interest rate calculations, particularly for discounting purposes. Creating the SOFR curve mirrors the methodology used for Fed funds and Libor curves – bootstrapping with highly liquid market quotes, including overnight rates, futures and swaps.

Since October 2018, CME has cleared SOFR swaps – notably SOFR OIS swaps (SOFR versus fixed rate) and basis swaps against the effective federal funds rate (EFFR). Figures 1 and 2 illustrate SOFR OIS swap rates and EFFR SOFR basis. If choosing the SOFR curve for discounting, SOFR rates can be exclusively derived from SOFR quotes, while basis swaps can construct the EFFR curve if required.

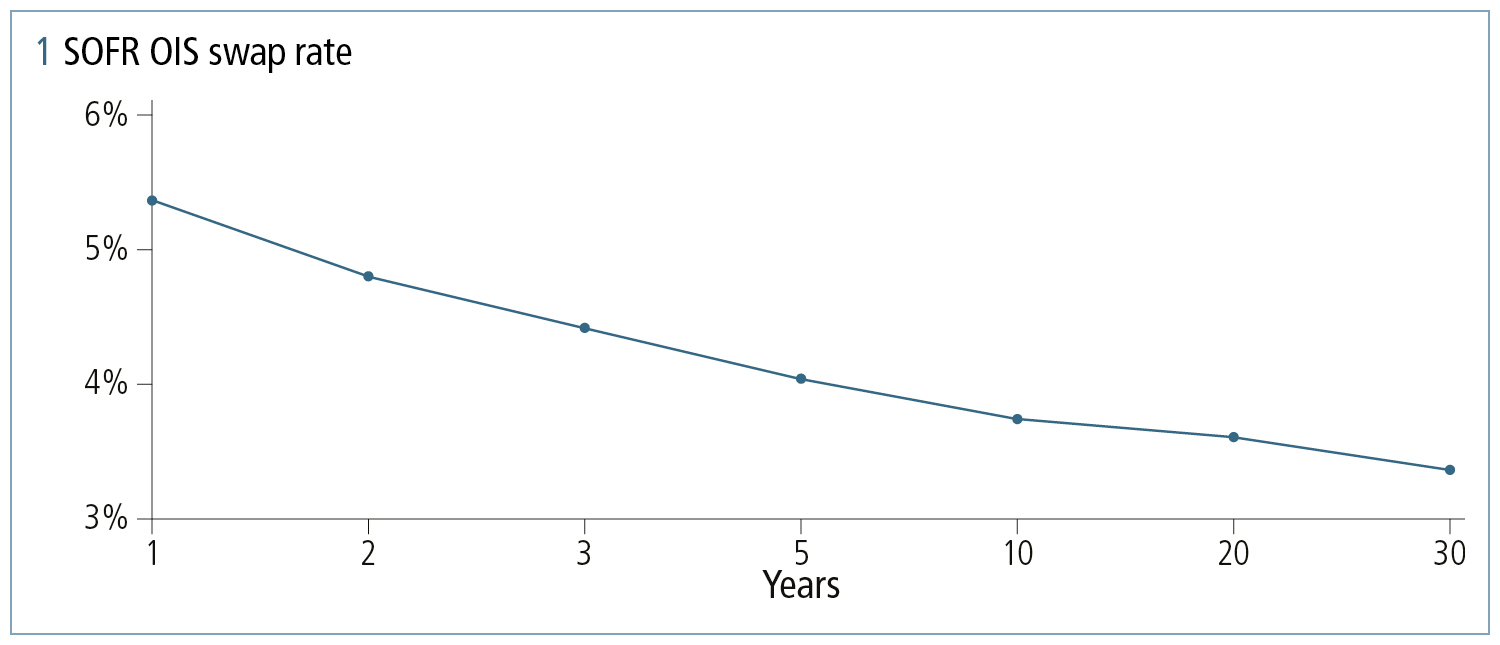
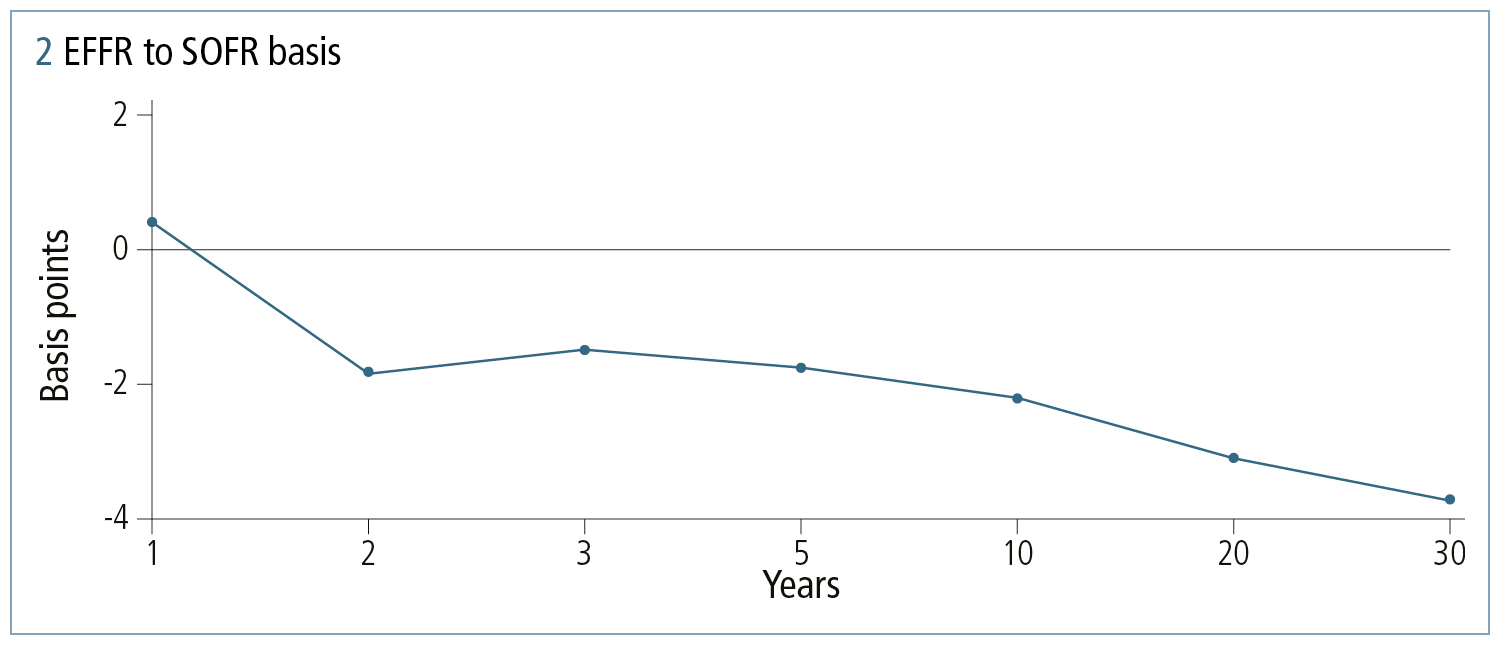
Calibrating the SOFR curve is more complex compared to EFFR and Libor. This is because of daily averaging, the retrospective nature of payments, geometric compounding and the necessity to include historical and projected segments in calibration to futures rates unique to SOFR.

To illustrate this point, let us consider the current three-month SOFR futures contract. As of August 2023, this contract is denoted as SR3M3, which began on June 22 and settled on September 20. The market quote reflects SOFR rates compounded from June to the current date, along with projected rates from the present to the settlement date. To put this in formulae, let’s denote the start date for compounding, which is in the past and is measured in number of business days from today, as $T_1^s$. The end-point of compounding, which is in the future, is denoted as $T_1^e$. The initial portion of the compounding process, spanning from the beginning to the current date, has already been determined and can be represented as a term denoted by $\prod \text{ℎ𝑖𝑠𝑡}$:

$$\prod \text{ℎ𝑖𝑠𝑡}=\prod _{i=T_1^s}^0\left(1+\frac{r_{t_i}\cdot n_{t_i}}{N}\right)$$

The formula for calibrating to the current futures price, ${\text{𝐹𝑢𝑡}}_{\text{𝑐𝑢𝑟}}$, involves projecting a flat SOFR rate, $R$, for the remaining period. The corresponding formula is:

$$1-\frac{{\text{𝐹𝑢𝑡}}_{\text{𝑐𝑢𝑟}}}{100}=\left[\prod \text{ℎ𝑖𝑠𝑡}\cdot \prod _{i=1}^{T_1^e}\left(1+\frac{R\cdot n_{t_i}}{N}\right)-1\right]\cdot \frac{N}{d_c}$$

Note that solving this equation for $R$ requires a root finder.

The above formulae use the following notations:

• •

  $d_c$ – the number of calendar days in the interest period.

• •

  $r_{t_i}$ – the SOFR interest rate applicable on business day $t_i$.

• •

  $n_{t_i}$ – the number of calendar days for which rate $r_{t_i}$ applies.

• •

  $N$ – the market convention for quoting the number of days in the year (in the US, $N=360$ while, in the UK, $N=365$).

Accounting for the convexity adjustment of forward-future rates is another challenge specific to SOFR rates. This adjustment reflects the distinction between the future rate, calculated under the risk-neutral measure, and the forward rate, calculated under the forward measure. Evaluating convexity adjustment requires rate volatilities – such as those obtained from implied volatilities of SOFR futures options quoted on CME.

Tackling curve complexity

To navigate the complexity of rate curves and products, financial institutions must either build their own analytics and risk systems or leverage third-party solutions. While the specifics of these solutions can vary considerably, they all must incorporate essential features to effectively address these challenges. These key features include:

• Comprehensive interest rate coverage across products – such as repos, bonds, futures, forwards, interest rate and cross-currency swaps, caps and floors, swaptions, curve options, and scripted interest rate payoffs and their numerous variations.
• Flexible curve construction for a range of market instruments, often with overlapping quotes that require joint fit or disentanglement, as well as modelling central bank dates.
• Live risk – particularly important for the buy side is the ability to observe profit and loss and basic rate sensitivity in live, dynamic updates.
• The ability to calculate sensitivities per curve, tenor and instrument used for the calibration, alongside the capacity to derive sensitivities to zero rates and reproject to instruments beyond those employed in the calibration process.
• Flexible interfaces to trading and risk management tools – such as Microsoft Excel spreadsheets or applications written in Python or Java – are very important for traders engaged in analysis and structuring activities.

Quantifi has developed a comprehensive solution to address the multifaceted challenges of interest rate curve construction, which meets the aforementioned institutional requirements. Quantifi has devised methodologies that demonstrate exceptional stability, precision and performance. This remains true even when tackling the complexities of concurrent calibrations that encompass four interrelated curves. Given multiple curves can sometimes form part of one global calibration, it is advantageous to regard them as a single object rather than a collection of several. This approach enables comprehensive analysis of the entire dataset simultaneously.

In addition to these features, Quantifi offers a number of other optimisation possibilities in curve construction. This includes support for advanced curve interpolation algorithms, including a range of spline techniques, and the ability to independently interpolate the short and long ends of the curve. From capturing the relationships between the term structures of the curves to computing sensitivities across various risk dimensions, Quantifi offers its clients flexibility and consistency.

 

Find out how Quantifi can help you optimise your interest rate curve construction and overall market and counterparty credit risk management

Download a copy of the Quantifi white paper, Mastering interest rate curve construction

Sponsored content