This article was paid for by a contributing third party.More Information.
Understanding options – A real-world example on the impact that skew can have on an options position

By Craig Bewick, Senior Director, Retail Sales, CME Group
The research views expressed herein are those of the author and do not necessarily represent the views of CME Group or its affiliates. All examples in this presentation are hypothetical interpretations of situations and are used for explanation purposes only. This report and the information herein should not be considered investment advice or the results of actual market experience.
One of the first concepts new options traders should be aware of is implied volatility (IV). If you search for the definition of implied volatility, the most common search engine result is “implied volatility represents the expected volatility (or price movement) of the underlying instrument over the life of an option”. Because IV represents the market consensus of what the price volatility of the underlying instrument will be it is indeed a very important concept to understand. Ceteris paribus, the higher the IV of an option, the more expensive or the higher the premium a seller will charge for that option and vice versa.
While IV is often described as an input to a standard pricing model, we prefer to think of it as an element that “falls out” or is derived from a pricing model. Of course, if one was performing a theoretical or academic exercise to determine the theoretical value of an option, they would, indeed, typically input an IV level into the model they chose in order to generate a theoretical value. Most options models incorporate the following inputs:
- Strike price of the option: Chosen by the trader (known)
- Days until expiration: Chosen by the trader (known)
- Price of the underlying instrument: Determined by the “market” (known)
- Interest rate: Generally, the accepted “risk free” rate (known)
“The unknown element to pricing an option is how much the underlying instrument will move between the execution of the option trade and the expiration of the option (implied volatility)”
Craig Bewick, Senior Director, Retail Sales, CME Group
All the above inputs are known to the trader. The trader can also determine what the current price or value of the option is because it’s generally a result of a bid/offer process, at CME Group it usually occurs on the Globex central match engine or the open outcry trading floor. The unknown element to pricing an option is how much the underlying instrument will move between the execution of the option trade and the expiration of the option (implied volatility). To illustrate, let us assume the current market in a given option is generically 3.5 bid at 4 offer. Next assume everything else stays constant but the market price for our option changes to 3 bid at 3.5 offer. Since the value of the option decreased and nothing else changed, we conclude that implied volatility, or the amount of movement in the underlying that the market is implying must have also declined.
Some traders use the straddle (long a call and put at the same strike) as a proxy for the volatility level in a given options market. This makes some intuitive sense if one thinks about putting on a speculative long straddle position. Since the long call in the position will increase in value as the price of the underlying goes up (again, and importantly, all else equal) and the long put if the price declines, the total premium for the straddle represents the magnitude of the price move required for the position to become profitable.
Options skew
Another, perhaps lesser known but important, concept in option pricing is that of options “skew”. This refers to the idea that different strikes and calls and puts, even on the same underlying and expiration, can trade at different implied volatility levels. This can be relative to different strikes within calls or puts or the relative value of calls versus puts. Historically, options skew was introduced to the market after the stock market crash in 1987, when options sellers began demanding higher premiums to protect against such “black swan” type events.
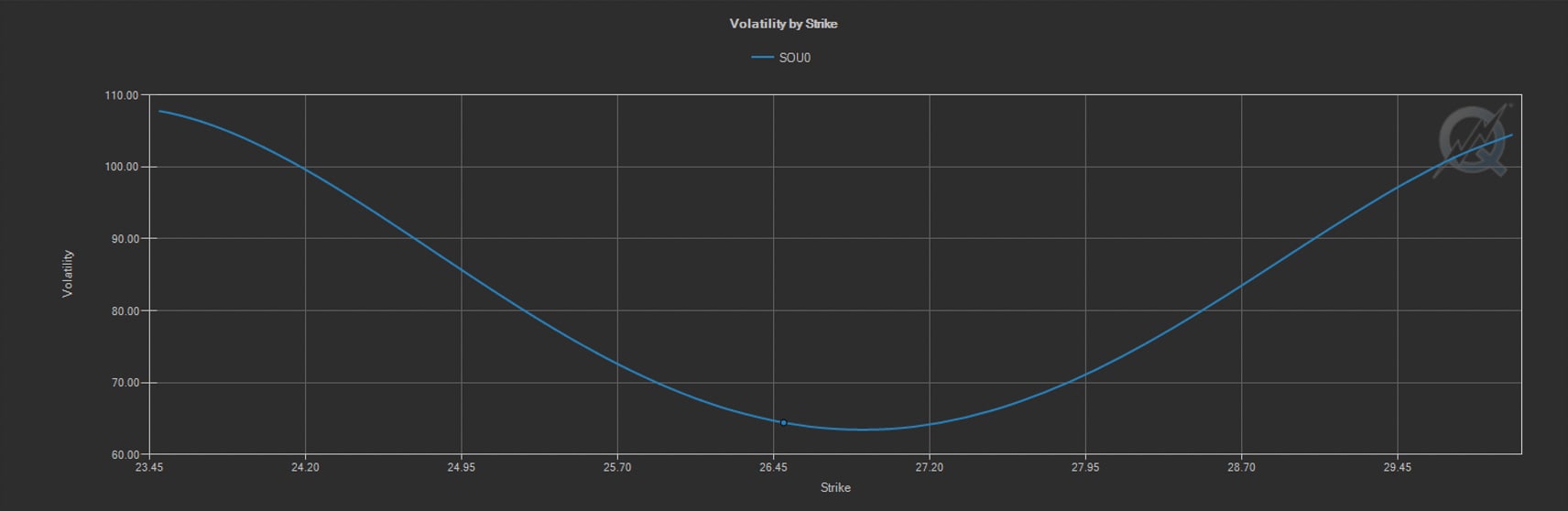
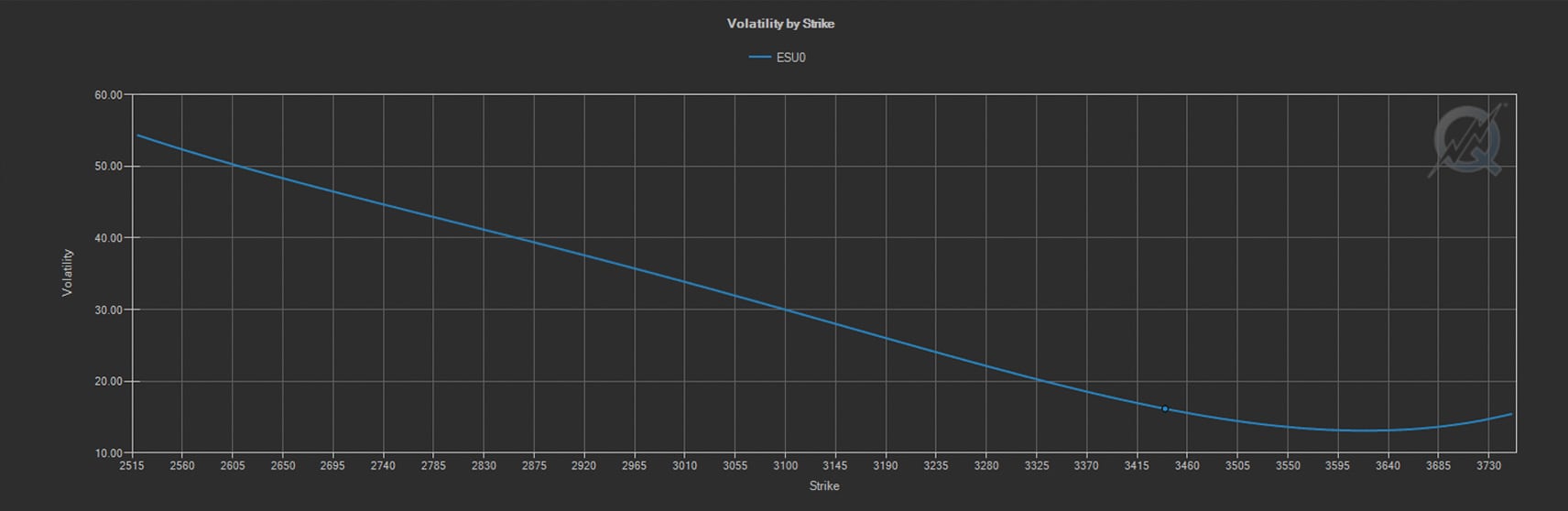
The shape of the skew curve differs among products based on the perceived likelihood of outsized moves in the price of the underlying. As you can see in these two QuikStrike® images, the skew in Silver options is much more a “smile” than the “smirk” in Equity options.
Risk reversal
Another proxy for measuring skew is risk reversal, a measure of the volatility in calls versus puts in a specific expiration. Before going deeper into the risk reversal, it’s important to understand a couple of basic options principles related to the relationship between calls and puts.
“One of the first options lessons some new professional traders learn is that ‘calls and puts are the same; they just have a different positive or negative sign’.”
Craig Bewick, Senior Director, Retail Sales, CME Group
Calls and puts maintain a price relationship with one another within a given option expiry. In fact, one of the first options lessons some new professional traders learn is that “calls and puts are the same; they just have a different positive or negative sign”. Perhaps the most effective way to explain the relationship is with a simple example of “put-call parity”. Put-call parity refers to the fact that the following formula must hold true, lest there would be arbitrage opportunities introduced into the market:
Call price – put price + strike price = Futures price
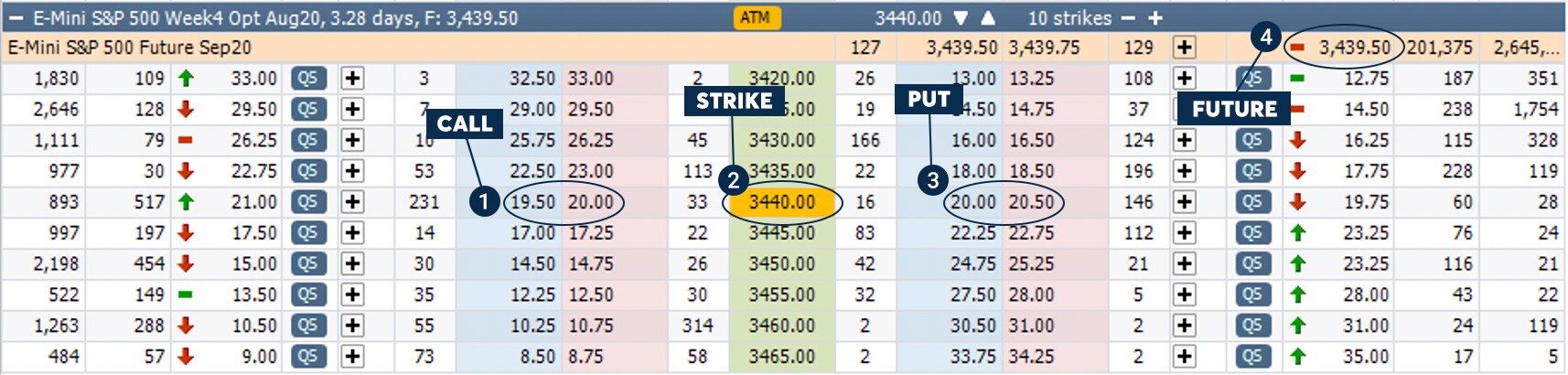
To prove our point, we took at snapshot from CME Group’s CME Direct trading front end (8/25, 8:10 AM Chicago Time) of the current market in the E-mini S&P 500 August Week 4 options:
Taking the mid-point of the call and put markets in the 3,440 strike, we find that the current prices:
- Call = 19.75
- Put = 20.25
- Strike = 3,440
- Future = 3,439.50
Which gives us the following equation: 19.75-20.25+3,440=3,439.50
Because of this relationship, if one were to buy a call and sell a put at the same strike, they would create a position with the identical P&L characteristics of a long future (and vice versa). Since this position would possess the same payoff characteristics as a long future, market participants are likely to quickly bring the prices back into line to capture any existing arbitrage if they were to diverge. In fact, in certain situations when CME Group futures experience a “locked limit” price move, the options markets may continue to trade and allow traders to discover a “synthetic” futures price.
A risk reversal is another name for buying a call and selling a put (or vice versa). These trades can be used to assume a speculative position in a market or can be used to hedge an existing position. Keep in mind, we showed an example that used the same strike in the call and put, which resulted in a position with a Delta value of 1.00 (like a future). Oftentimes, traders will initiate risk reversal positions using out of the money options, which will also result in directional positions but with beginning delta values of less than 1.00.
“Oftentimes, traders will initiate risk reversal positions using out of the money options, which will also result in directional positions but with beginning delta values of less than 1.00”
Craig Bewick, Senior Director, Retail Sales, CME Group
Risk reversal – A real world example
The recent spike in silver prices, Silver options volatility, and the corresponding relative increase in call volatility versus put volatility provides us with a great opportunity to highlight the importance of skew and ways to create a potential trading opportunity in the options markets. As we stated earlier, a trader could use a risk reversal position to assume a speculative long or short position in the underlying instrument or use it to hedge an existing position. We are going to go through a hedging example because of the illustrative power it creates.
Background
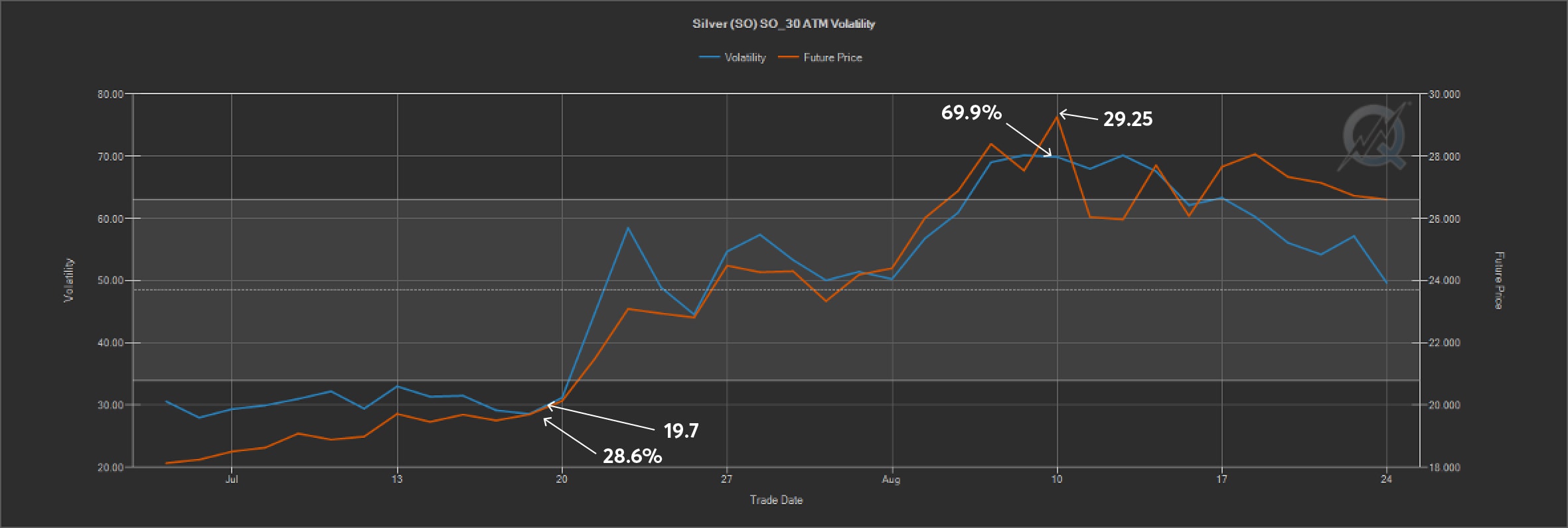
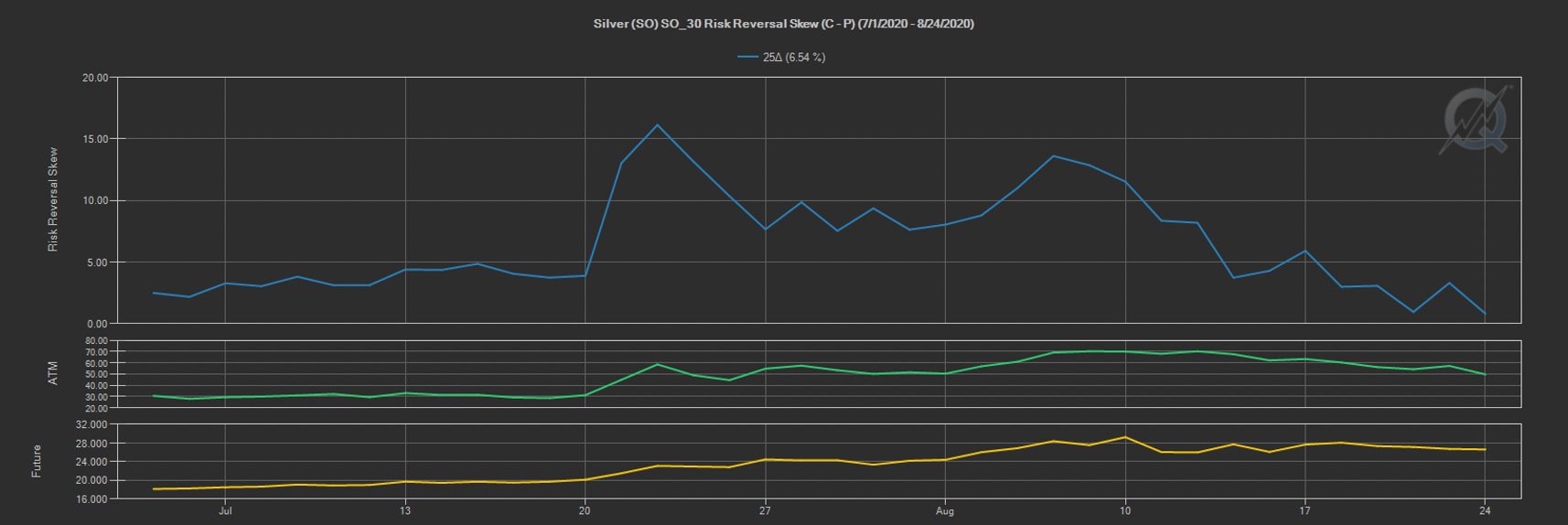
As you can see in the QuikStrike® image below depicting implied volatility and price in the Silver market, in the span of a few weeks, the price of Silver futures rallied from 19.7 to 29.25 and 30-day volatility in the options markets rallied from 28.6% to a historical high of nearly 70%.
Simultaneously to these increases, the implied volatility in the 25-delta calls spiked relative to the puts, as you can see in the blue line in this QuikStrike graph that depicts simply the call volatility minus the put volatility.
Because of the dramatic increase in the volatility of the calls relative to the puts (remember, all else equal, that also means the value or premium of the calls increased relative to the puts), we took a look at the impact that this would have on the P&L of a short risk reversal versus a long futures position in the Silver market.
As we discussed before, in order to assume a short risk reversal position, one may take action on being able to sell the relatively high volatility in the calls and buy the relatively low volatility in the puts.
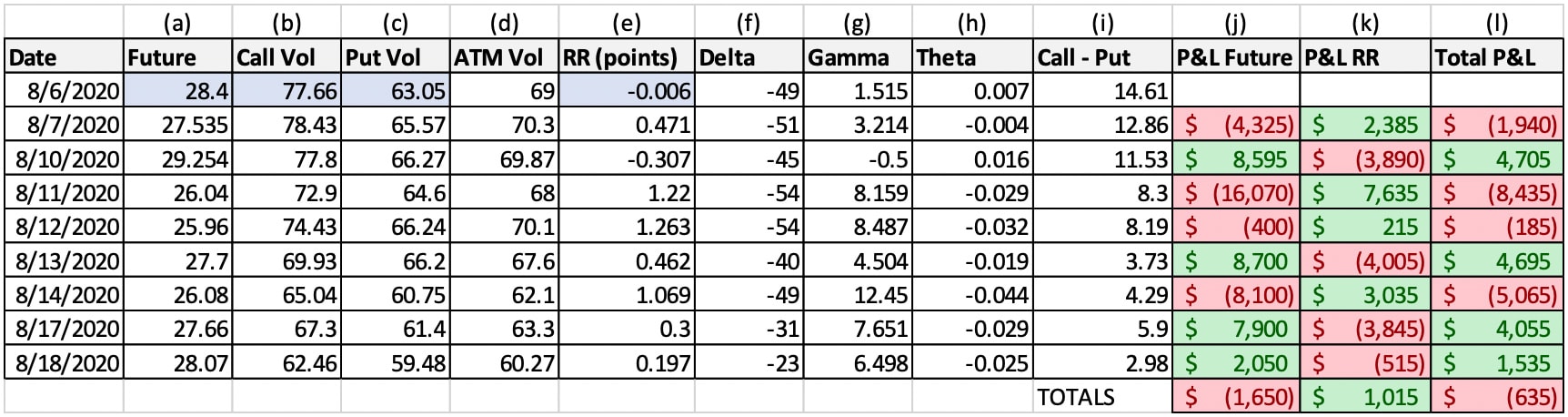
We used QuikStrike® options pricing analytics and historical data to replicate the theoretical value of a futures position versus selling a 25-delta call and buying a 25-delta put on August 6, 2020 in CME Group Silver markets
Assumptions (shaded in BLUE):
- Long Silver futures position at 28.4
- Short 25-delta call at IV = 77.66%
- Long 25-delta put at IV = 63.05%
- Resulting in an initial execution price in the options of a credit of .006 or $30
In order to keep our example manageable, we used the historical values for implied volatility and price that occurred in the Silver market, but did not make any adjustments to our position as a professional trader might do. This is an exercise in theoretical options values to emphasize the impact that skew can have on an options position.
The following chart shows the price and volatility moves along with the corresponding theoretical Greek and position P&L values:
As you can see, at the time of execution (on 8/6), the 25-delta risk reversal has a delta value of -49. Since the long futures position has a static delta value of +100, the risk reversal provides a partial hedge to the long futures position against a potential downward price move.
- On the days that the price of the future declines (column a), the P&L of the futures positions declines (column j) while the P&L of the risk reversal increases (k).
- We included the Greeks so that you can see how the position is impacted as the price and volatility move. Typically, options traders would adjust the position based on these measures, but as we said, we’ve kept the position static for illustration purposes
- Total P&L of long futures position -$1,650
Total P&L of risk reversal position +$1,015
Total P&L = -$635
So, absent the risk reversal hedge, the long futures position would have had a theoretical loss of $1,650 and because of the hedge, the theoretical loss was reduced to $635.
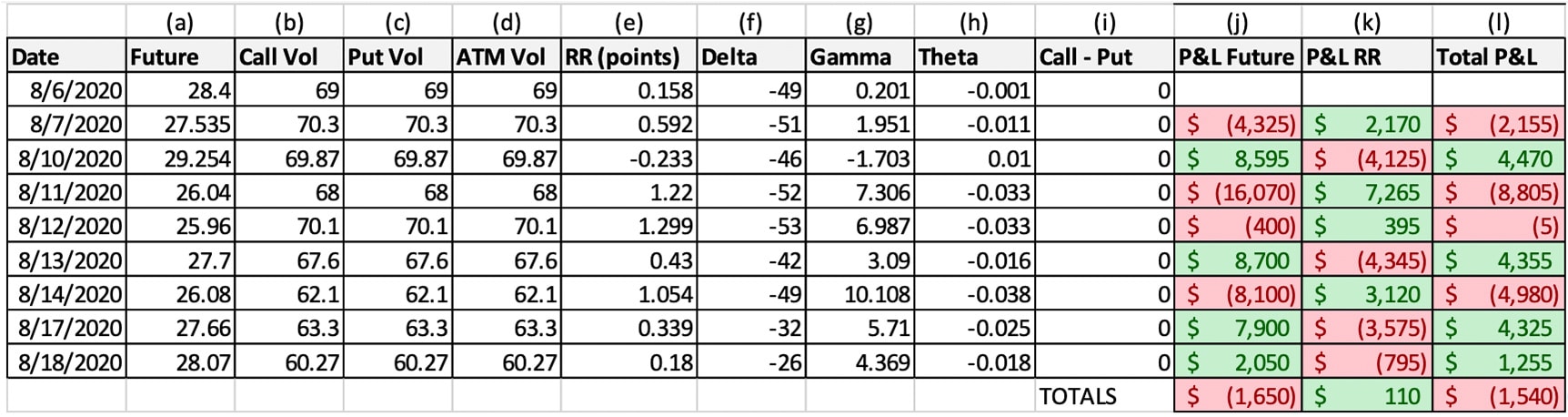
Now, let’s look at the theoretical value of the risk reversal if we remove skew from the Silver options market. To do this, we selected options strikes on 8/6 that would carry a delta value of about 25, if we used the at-the-money volatility for both the call and put. Again, we are not making any adjustments to the position based on Greek values, and we’re assigning the call and put the same volatility throughout the time period, so this is an exercise in theoretical value, but serves a very nice illustrative purpose.
As you can see, when the risk reversal is initiated at a level absent of skew, the theoretical, overall P&L of the position drops to -$1,540 from -$635.
Why the difference?
When we initiated the original risk reversal, the calls (which we sold) were trading at a vol 16.6% higher than the puts (which we bought). So, while both risk reversal positions gained because the price of the underlying declined (negative delta), the original position also gained as call volatility declined relative to the puts.
Let’s take a closer look:
- On 8/7 the call minus put volatility dropped from 14.6% to 12.86%; the original risk reversal gained $2,385, while the “skew-less” position gained $2,170.
- On 8/11 the call minus put volatility dropped from 11.5% to 8.3%; the original RR gained $7,635, while the “skew-less” position gained $7,265.
- On 8/14 the call minus put volatility dropped from 8.1% to 3.7%; the original RR lost $4,005, while the “skew-less” position dropped $4,345.
Conclusion
Again, this was an exercise in theoretical options value. Realistically, some traders would manage the positions we initiated based on the “Greeks” and other factors. However, we believe it does a nice job of underscoring how important it is to understand, not only volatility, but also the relative volatility (value) of different options to one another.
Of course, this paper has the invaluable benefit of being able to look back at the market to see what happened. In real life and trading, there is no way to know that even though the risk reversal had gotten extremely large (call volatility was trading far higher than put volatility) that it wouldn’t continue to grow even bigger.
Stay in the know
Get timely information and insights to help you make your best trades with the daily InFOCUS futures and options newsletter.
Sponsored content
Copyright Infopro Digital Limited. All rights reserved.
As outlined in our terms and conditions, https://www.infopro-digital.com/terms-and-conditions/subscriptions/ (point 2.4), printing is limited to a single copy.
If you would like to purchase additional rights please email info@risk.net
Copyright Infopro Digital Limited. All rights reserved.
You may share this content using our article tools. As outlined in our terms and conditions, https://www.infopro-digital.com/terms-and-conditions/subscriptions/ (clause 2.4), an Authorised User may only make one copy of the materials for their own personal use. You must also comply with the restrictions in clause 2.5.
If you would like to purchase additional rights please email info@risk.net