
This article was paid for by a contributing third party.More Information.

FX volatility – An evolutionary story

History
What is volatility? The word itself has a noble origin – the Latin volatilis has several meanings, including winged, flying, swift and fleeting – and is derived from the verb volare, to fly. In modern English, the word volatility is also concerned with movement, variation and also risk. A volatile liquid is easily vaporised; a volatile person is inconstant, fickle, given to mood swings; a volatile situation is unstable and potentially violent. And a volatile market is one that experiences large and unexpected swings in value.
In science, an everyday word can often be expropriated and given a very precise meaning. An example of this is ‘force’ or ‘power’, both of which have mathematical definitions. Finance is no different. When Black, Scholes and Merton developed their model of market movements in 1973, they assigned a mathematical definition to market volatility. From that moment, in the valuation world, volatility has been defined as the standard deviation of the log of the changes in value, over a specified period. This was an interesting choice; it embeds several assumptions into the methodology of option valuation, not all of which are fully justified.
Firstly, it is not directional. Moves upward are just as ‘risky’ as moves downward. Then, the use of a standard deviation indicates that the market moves are lognormal. This is a reasonable approximation under some circumstances, but tends to fall apart when larger moves are considered. But the choice of definition was inspired. It meant that market movements could be put into the same category as the random movement of atoms in a gas – Brownian motion – and this allowed a well-understood branch of mathematics to be applied to valuing financial contracts like options. Overnight, the art of pricing options became a science.
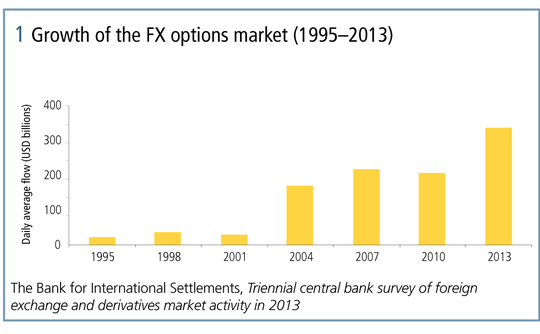
In 1983, Garman and Kohlhagen published the relatively simple extension to the Black-Scholes-Merton model, which – by including both foreign and domestic interest rates – enabled it to be used for foreign exchange. Since then there has been a seemingly inexorable rise in the FX options market, with no sign of it slowing down. Figure 1 presents the results from the Bank for International Settlements’ Triennial central bank survey of foreign exchange and derivatives market activity in 2013, when more than USD300 billion equivalent of options were traded each trading day.
Were the first models right?
From the increase in flow, one would say that something had gone right with the models. And yet, the original model had numerous shortcomings, which subsequent modifications could not entirely ameliorate.
The volatility in the models refers to the volatility of future price movements, over the lifetime of the deal. Initially, it was assumed that the future volatility would be the same as the recently realised volatility. So, if the volatility for a one-month option was needed, it could be calculated by looking at the data for the previous month. This future volatility is known as the implied volatility, as it may be implied mathematically from the price of the option. However, as the market became more widely traded, traders began to deviate from this practice, using their own views of upcoming events to assign a volatility to the future period. They had good reason to do so, as realised volatility is not even close to constant and varies widely. Today, implied and realised volatility are not the same. On average, implied volatility is a little higher than realised, particularly for short-dated options.
The next major modification came after the stock-market crash in 1987. Moves occurred to which the Black-Scholes-Merton model had assigned near-zero probabilities. And so, the volatility smile rose to allow traders to express a view that the market might move further than the traditional model allowed. The smile refers to the volatility graph as a function of strike – it is usually lowest when the option is struck at the forward rate. It can then curve up at the sides, indicating a higher implied volatility for large moves. The traders may think ‘if the market moves that far, it will be more volatile’. Mathematically, this neatly assigns higher probabilities to larger moves than those obtained from the normal distribution assumed in the original model.
As an additional twist, the smile can vary with tenor, allowing traders to express their views of market activity at different times in the future. Figure 2 illustrates how implied volatility varies with strike and tenor, showing what a long way we have come since the flat surface of the early days of the FX options market. The three axes are the implied volatility, the tenor and the strike. The latter is given in terms of the parameter delta (d); 30d indicates that the model predicts an approximately 30% chance of the rate ending up there at the end of the deal. The most liquid option strikes are at-the-money (ATM), 25d or 10d.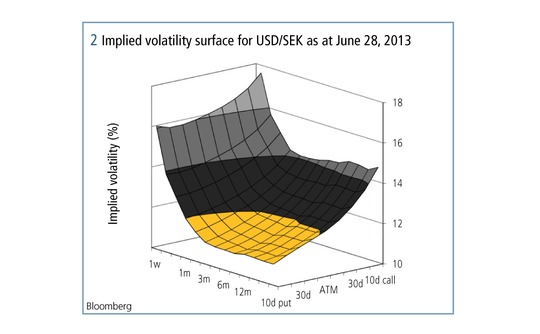
Are the current models right?
With these modifications, can we say that FX option valuation models are ‘right’ today? If, by ‘right’, one means whether they reflect what the market really does, then the answer is no. If the option valuation process was perfectly efficient, then one would not find any systematic over- or underevaluation of options in the market. On average, what you paid for an option in premium would be what it returned in payout after costs. But this is not what happens.
Looking to figure 3 to understand further, each bar in the graph represents the average payout-to-premium ratio for FX put and call options of the specified currency pair. Combinations of put and call options are studied to reduce the effect of trends in exchange rates. The yellow bars are at-the-money-forward (ATMF) options, the black are 25d options and the grey are 10d options. So, the yellow bars represent whether ATMF options are good value for money, and the black and the grey whether out-of-the-money (OTM) options are good value.
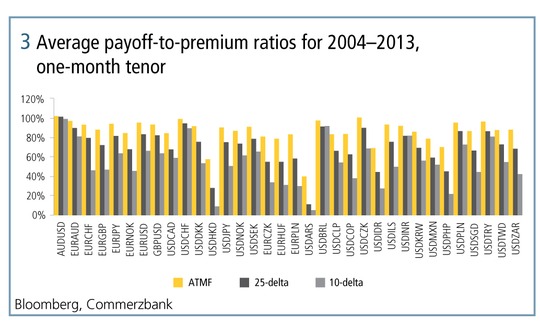
If all were fair value – if the market were perfectly efficient – then all of these bars would lie close to 100%, but what we see is almost all of them are less than 100%, and that the OTM options are much worse than the ATMF options. On average, the payout for ATMF straddles is only 86.7%, for 25d strangles it is 71.8%, and for 10d strangles it is 58.0%. This is far from perfect efficiency.
Where the anomalies lie
Two facts can be extracted from this data. The first is that these short-dated options are, overall, poor value for money. The second is that OTM options are of lesser value than ATMF, and this effect increases with the distance of the strike from the forward. The implied volatility is a little too great for ATMF options and much too great for OTM options.
This leaves us with more information than we started with. As a hedger, we now know that ATMF options are better value than their apparently cheaper counterparts. And, as an investor, we can see some opportunities to generating return. In this era of rising volatility, both are becoming more important. The evolution of the FX option market is far from over.
Read/download the article in PDF format
The views expressed in this article are those of the authors and are not necessarily the view(s) of Commerzbank, and this communication has been prepared independently of Commerzbank. No representations, guarantees or warranties are made by Commerzbank with regard to the accuracy, completeness or suitability of the data.
Sponsored content
Copyright Infopro Digital Limited. All rights reserved.
As outlined in our terms and conditions, https://www.infopro-digital.com/terms-and-conditions/subscriptions/ (point 2.4), printing is limited to a single copy.
If you would like to purchase additional rights please email info@risk.net
Copyright Infopro Digital Limited. All rights reserved.
You may share this content using our article tools. As outlined in our terms and conditions, https://www.infopro-digital.com/terms-and-conditions/subscriptions/ (clause 2.4), an Authorised User may only make one copy of the materials for their own personal use. You must also comply with the restrictions in clause 2.5.
If you would like to purchase additional rights please email info@risk.net