Don’t fear the clearer

The wider use of CCPs is not a systemic threat – but participants do face hard-to-measure risks

The perils of widespread central clearing are real – system participants accept hard-to-fathom credit and liquidity exposure – but our analysis of this complex network suggests the tail risks are often overstated. Larger clearing members have enough capital to weather a crisis. Admittedly, smaller firms could be submerged in the waves created by a fellow member’s default, but even a chain of such losses would not threaten the system as a whole.

These conclusions are not easy to draw, and warrant further investigation.  

Assessing the systemic risks of central clearing is difficult because the system resembles a network of interconnected hubs – each central counterparty (CCP) has dozens or hundreds of members, the larger ones of which are also members of many other CCPs and act as intermediaries for many more clients. Each member firm is blind to the exposure that is funnelled through each of its peers, and relies for its own safety on the variation margin, initial margin (IM) and default funds that are calculated and collected by the CCP.

Should a member collapse, losses that exceed its own IM and default fund contributions will be borne by other members, and feedback loops could be triggered: the initial loss could produce other defaults within the system; CCP rules requiring the replenishment of default funds increase this danger; and market volatility hikes margin requirements, piling yet more pressure on clearing participants. These effects make it harder for a CCP to auction off the portfolio of a stricken member – the easiest way to return a clearing house to a balanced position – and could increase member losses.

One of the very important potential breaking points, seldom mentioned in conjunction with central clearing, is the fact that CCPs can be depositors of the same banks that, as clearing members, contribute to the IM and the default fund. Many of the larger banks also provide settlement and investment services to CCPs, as well as credit and liquidity lines. If such a bank were to default, the second order effects would be very painful. As Juvenal asked a long time ago, “quis custodiet ipsos custodes?”.

Some of the risks associated with the use of CCPs can be mitigated by applying distributed ledger technology (DLT) and smart contracts. But this will not be simple – or cheap (see box: Using DLT to reduce clearing risks).

Natural complexity

Although the system of interconnected CCPs is far too complex to be described analytically, it is not beyond reach to study it numerically by developing simulation models that capture the contingent cashflows (including those related to margining and defaults) between all agents.

Given the size and interdependency of the entire network of CCPs and clearing members, our model, which was originally published by Risk.net in 2017 and expanded in last year’s Margin in Derivatives Trading, is naturally complex, yet it provides some important insights, both qualitative and quantitative. In particular, it shows there are material feedback loops between defaults of clearing members and market volatility that must be captured in order to realistically assess default losses and contingent liquidity requirements.

In order to build a proper model for a CCP or – even harder – a system of CCPs, a modeller needs to describe the following effects: (a) the asymmetry of information due to the fact that a clearing member is exposed through its default fund contribution to losses on a proportion of the defaulting members’ entire portfolio; (b) a feedback mechanism that intrinsically links clearing member default, market turbulence and liquidity calls on market participants, so expected loss becomes strongly path-dependent; (c) the individual nature of different member firms, varying from large diverse financial institutions where clearing makes up a small amount of their business, to proprietary funds for which a default event will be driven purely by margin calls on cleared trades; (d) the individual aspects of each CCP, including their initial margin and default fund methodologies, loss allocation process, waterfall and assessment rules; (e) the interconnectedness of the CCPs themselves due to the fact that the default of a major clearing member is likely to affect several CCPs simultaneously and may have knock-on effects; (f) the changes in IM and default fund requirements as the system evolves, which are particularly important for liquidity considerations (see figure 16.3 below, from chapter 16 of Margin in Derivatives Trading).

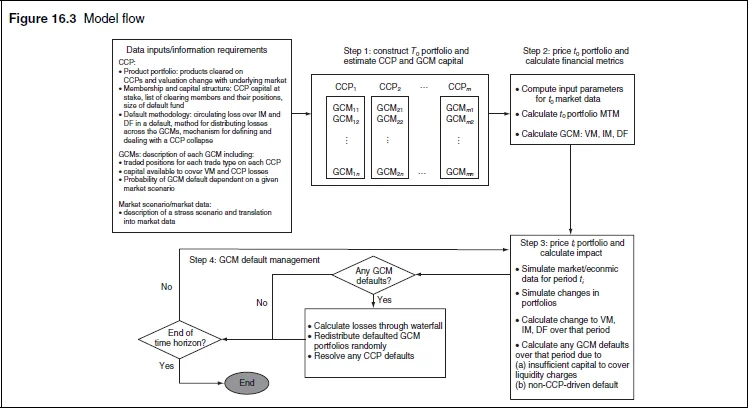
Portfolios of typical CCP members consist of numerous long and short trades with slightly different characteristics (eg, maturity, coupon, strike, etc), which wholly or partially cancel each other. We refer to the total notional over long and short positions as the “gross” notional, and the difference as the “net” notional. We emphasise that risks are ultimately determined by net positions, so net notionals are of primary concern. However, gross notionals should not be discarded, since they provide useful and important information on accumulated historical volumes.

Typically, CCPs publish gross notionals aggregated across all members for certain categories of derivatives that are discriminated by the type of trade, currency and tenor. A representative example would be the aggregate gross notional for fixed-versus-six-month-floating Euribor swaps for tenors in the range of two to five years (alongside other aggregates).

We used these aggregates as a measure of the relative scale of the exposures of the CCP to different trade types, currencies and tenors. To exploit all relevant available information, we aligned our methodology to the categorisation used by the CCPs when reporting the corresponding aggregate gross notionals. We developed a randomisation scheme exploring the space of valid configurations of the unknown positions of other clearing members, satisfying the known constraints, including values related to the positions of a hypothetical clearing member, XYZ, and the aggregate gross notionals published by the CCPs.

For a fixed time horizon, we are interested in two random variables η_C and η_L; representing credit losses due to defaults (of other clearing members and CCPs) and potential liquidity drains for XYZ respectively. These variables are scaled by the shareholder equity of XYZ, and hence represent the relative significance of losses and margin calls to the capital buffer, which is set to $300 billion, approximately the same size as the shareholder equity of the big four US banks.

The quantification of feedback between market volatility and probability of default calls for constructing the complementary cumulative distribution functions (CCDFs) for η_C and η_L. In order to compute CCDF_C and CCDF_L properly, the contingent cashflows between all agents in the CCP network should be taken into account. We calculated these distributions under two different scenarios: (a) defaults only; and (b) defaults causing increase in market volatility through a feedback-based regime-switching mechanism (see figures 16.6 and 16.7).

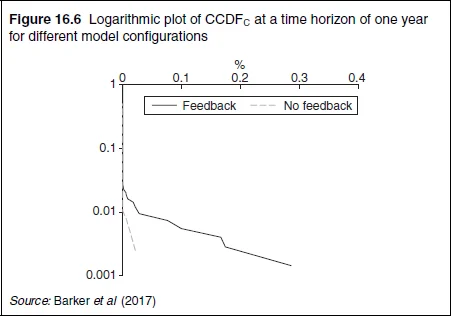
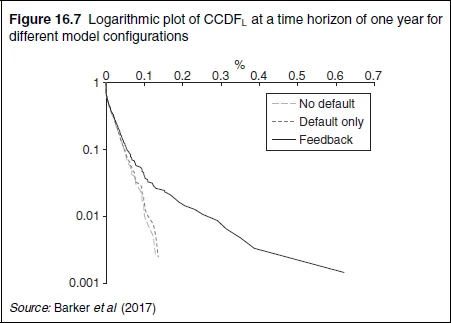
Our calculations demonstrate four key points: (a) the feedback loop in our model correctly captures the natural wrong-way risk between defaults and market volatility, and dramatically amplifies the tail of the loss distribution due to defaults; (b) even making conservative assumptions about the relationship between defaults and market volatility, and taking into account the interconnected and complex relationships between the agents within the CCP network, defaults do not generate losses large enough to threaten the survival of a well-diversified and well-capitalised financial institution simply because its clearing activities constitute a relatively minor part of the overall business mix; (c) however, smaller clearing members can certainly be wiped out by failures of other member firms, especially large systemically important ones; (d) in dollar terms, liquidity drains due to margin calls are an order of magnitude or more larger than losses due to default.

To illustrate the last point, our model shows the ratio of losses due to default to a bank’s equity is 0.02%, while the ratio of the incremental change in initial margin to a bank’s equity is 0.3% – this is calculated to a 99% confidence level, over a one-year horizon. For a hypothetical systemically important bank with market capitalisation of $300 billion, default losses and liquidity drains are $60 million and $900 million respectively.

Post-crisis regulation

In summary, regulatory changes since the 2007–10 global financial crisis have resulted in a significant increase in the volume of centrally cleared financial instruments. Yet the risks associated with central clearing are relatively poorly understood, not least because of the technical difficulties in building a suitable theoretical framework.

Our framework allows one to simulate the realistic contingent cashflows between all the agents in the CCP network and to estimate the associated risks. Our results indicate that tail losses and increased liquidity requirements are very real and, moreover, that liquidity requirements – margin calls – dominate those related to credit risk.

The often-mentioned fear that the wider application of central clearing to over-the-counter derivatives has a destabilising impact on the financial ecosystem as a whole because of contagion effects transmitted through the CCP network is not supported by our numerical simulations. While this result is at odds with received wisdom, it can be explained by the fact that losses due to default are a small fraction of the Tier 1 Common Equity of the diversified financial institutions that dominate the CCP membership.

Our recommendation to clearing members assessing the risks and costs associated with their central clearing activities is to focus primarily on funding and liquidity requirements, which, if not provisioned for, can negatively affect business as usual. Still, by their very nature, any CCP-related losses are likely to be realised precisely under extreme market dislocations, making their absorption particularly painful to the clearing members.

Using DLT to reduce clearing risks

The findings of our analysis are a mix of good and bad news: at present, the clearing system is unlikely to amplify institution-specific problems to the point they become a systemic threat. But it could extend a crisis and the degree of collateral damage involved. So, what can be done to limit these dangers?

Distributed ledger technology (DLT) offers an attractive alternative, or at least a viable complement, to the one currently used by CCPs. At present, there are three necessary steps required to trade public securities: (a) buyers and sellers have to be matched; (b) the transaction has to be cleared, that is, novated to a CCP; (c) the transaction has to be settled, that is, delivery versus payment (DvP) has to take place so title and money can be transferred as expected. These steps are characterised by vastly different time scales – trading often takes place in milliseconds, while clearing and settlement take 1–3 days. The actual process is very involved and includes investors, custodial banks, exchanges, clearing members, CCPs, central securities depositories, regulators and others.

To its credit, the current set-up provides adequate solutions to the following problems: (a) counterparty credit risk management; (b) netting; (c) DvP and credit risk more generally, which is addressed by collecting variation margin, initial margin and default fund contributions from clearing members; (d) anonymity; (e) ability to borrow. However, numerous issues remain: (a) cost; (b) speed; (c) the need for reconciliation; and (d) frequent failures.

The status quo irritates many people, who are pushing towards instantaneous settlement infrastructure. Potentially, a DLT-inspired design of exchanges can improve the overall process, making it more stable and less costly.

It is clear that straightforward attempts to apply DLT to clearing and settlement cannot be successful, though. The reasons are simple – instantaneous settlement obliterates all the aforementioned advantages of the current system. It increases the money sloshing around by at least an order of magnitude because there’s no prospect of netting off if all transactions are settled instantly, which can cause considerable problems if one of the payment legs fails for technical or other reasons.

However, by using permissioned private ledgers, one can certainly cut costs, somewhat increase speed of clearing and settlement, and reduce the number of failures and hence the need for reconciliation. In particular, smart contracts, if they can be legally enforced, can help with DvP, provided both securities and cash are parts of the same ledger. Thus, by shortening and streamlining settlement process, DLT will help to suppress potential liquidity drains and make clearing members’ defaults much less traumatic then they are now for the system as a whole. If taken to its logical limit, it can eliminate the need for central clearing in the first place, thus potentially alleviating the dangers related to a single point of failure in the financial system as a whole.

Alexander Lipton is chief technical officer at SilaMoney, MIT Connection Science fellow and a visiting professor of financial engineering at EPFL in Lausanne. He is a contributor to Margin in Derivatives Trading, published in 2019 by Risk Books.