Cutting Edge introduction: requiem for a probabilist

The already challenging task of calibrating stochastic volatility models becomes even more complex when rates are random too. But an efficient Monte Carlo approach can be found – by using an esoteric, but neglected, stochastic calculus. Laurie Carver introduces this month’s technical papers

Paul Malliavin, a French mathematician who died in 2010 aged 84, was working on an esoteric problem in pure probability in the 1970s – under what conditions the distribution of a random variable is smooth – when he discovered one of the revolutionary ideas of stochastic analysis. His breakthrough has been largely ignored by finance practitioners, but the first of this month’s technical papers – Being particular about calibration, by Société Générale’s Julien Guyon and Pierre Henry-Labordère – makes use of what is known as the Malliavin derivative.

The distributions Malliavin was interested in were of the end points of stochastic processes such as Brownian motion. He wanted to see how this distribution function changed as the path of the process changed. In proving the result he had wanted, he stumbled on to a new calculus that extended Newton’s into the realm of the random.

There are natural quantities you might want to know about a random path – the area beneath it, or its length, or if the path represents a stock price, an option payout, for example. Malliavin’s genius was to show how to quantify their sensitivity to a small change in the path. Part of what makes this so remarkable is that it is an inherently infinite dimensional problem – the function can in principle depend on any of the uncountably many points along the path.

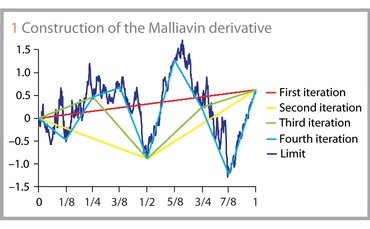
An intuition can be grasped for the Malliavin derivative using a kind of thought experiment (see figure 1). First, pick a point in the plane, with co-ordinate 1 on the x axis, at random: now draw a line from the origin and apply the function to this path. Because it will only depend on the one point, the sensitivity can be calculated using normal Newtonian calculus.

Now pick another point, with co-ordinate 1/2 on the x axis, at random; draw a line from the origin to this point, and from there to the first random point. Again, the function’s sensitivity to these two points can be calculated. Then fill in with points at 1/4 and 3/4 and re-calculate; then 1/8, 3/8, 5/8, 7/8, and so on. In the limit, these points will determine the continuous random curve, and the complete sensitivity will be known.

I think it's still thought of as more complicated than it actually is. Some of the early presentations were quite scary and technical

While Malliavin was working, mathematical finance was in its infancy, but was fast becoming a hot research area. Option pricing of course involves calculating expectations of stochastic processes. Their sensitivity to changes in the underlying’s paths have names – delta, gamma, rho, vega: the Greeks. Traditionally, these are calculated by shifting the underlying parameters a small amount and recalculating the expectation – a clumsy and possibly numerically intensive procedure, especially for discontinuous payouts such as digital options.

But in the 1990s, researchers applied Malliavin’s calculus to more efficiently calculate the Greeks of generic stochastic volatility models. By multiplying the option payout within the expectation by a certain new process called a ‘Malliavin weight’, all sensitivities can be found. It is similar to a method of ordinary calculus called integration by parts, though crucially it does not require the probability density of the process to be known.

Guyon and Henry-Labordère use the Malliavin calculus to facilitate calibration of models for which both volatility and interest rates are stochastic. By noting that a crucial term in their calculations can be considered as a digital option, and using the Malliavin derivative to replicate it, the authors simplify it to a more easily computable form – and hence calibrate quicker than a traditional approach.

“Usually, when you have a non-smooth payout like a digital you can use Malliavin calculus to get something smoother,” says Henry-Labordère. “In our case, we actually use it to get a more singular payout that, perhaps counter-intuitively, improves the computational time of the calibration.”

However, few other industry quants have so far taken to using the calculus. This is partly because it has a fearsome reputation for being heavily technical. “I think it’s still thought of as more complicated than it actually is,” says Bernt Øksendal, professor of mathematics at the University of Oslo. “Some of the early presentations were quite scary and technical, so people thought the costs would outweigh the benefits.” He is promoting a simpler approach based on expanding payouts as sums of more easily manipulated functions.

There are also concerns that practical problems may prevent Malliavin calculus being useful. “You are essentially exchanging the noise from bumping for more Monte Carlo noise – this won’t always be smaller,” says Jesper Andreasen, universal head of quantitative analytics at Danske Bank.

But Malliavin continues to inspire new work, with notable avenues of research open in applying his findings to jump processes, and extending them to highly path-dependent option payouts, quants say. His financial legacy may turn out to be greater than some once thought.