The equity-to-credit paradigm

Convertible bond pricing used to be a specialist niche, where all that mattered was to have a good handle on the prospectuses and to know how to translate, in quantitative language, their often complex terms and conditions.

Roughly speaking, the convertible bond was assimilated to a bundle of fixed income component (the underlying corporate bond) and equity option component (the right to convert into the underlying share), and the theoretical valuation proceeded accordingly. On closer inspection, the contingent part had to be decomposed into a sequence of options, as the holder's right to convert was often accompanied with the issuer's right to call back the bond as soon as the call protection period expired or, ultimately, with the holder's right to sell back the bond at predetermined put prices, at predetermined discrete dates. Despite the subtlety of their logic, these clauses were well within the reach of standard dynamic programming techniques, and the general-purpose binomial or trinomial trees flourished as the favoured tools to address a broad spectrum of non-vanilla products, ranging from the American put, to the typical barrier option, to the convertible bond.

Convertible bonds, however, soon broke away from the rest of exotic products as they enjoyed liquidity almost comparable to the vanillas. They fell into a class of their own - the peculiar class of highly standardised yet highly complex structures. Doubtless their popularity among volatility arbitrage houses (which sometimes dedicated themselves exclusively to convertible bond strategies like the convertible bond specialists hedge funds) must have contributed to their liquidity and standardisation. Thus, the demand became pressing for quantitative tools that could handle the complexity of the convertible bonds, yet produce theoretical values and Greeks as robust and reliable as the vanillas.

This signalled the demise of the tree as numerical engine and prompted the development of advanced numerical schemes, based on the partial differential equation techniques and adapted to the convertibles. Accuracy and speed could only be achieved by engineers trained in computational methods that were, at the time, foreign to quantitative finance, and the opportunity emerged for talent specifically combining financial theory and numerical expertise. This is the area in which IT^O33 first became known and later established itself as the leading provider of advanced convertible-bond pricing engines.

Despite the inner complexity of the convertible bonds, their pricing framework would have remained simple if the agenda had only been one of coverage of their multiple features. Indeed, another difficulty soon emerged and, although it may have appeared at first to be specific to the convertibles, it quickly spread to the whole class of equity derivatives. Basically, it consisted of the necessity of modelling the credit risk of the issuer of the convertible, and not just the volatility of the underlying equity. Convertible bonds were the natural candidates for such a hybrid equity-to-credit process, because their bond component was subject to credit risk like the rest of corporate bonds, and because their equity option component could no longer be priced separately as a consequence of the optimal conversion policy.

The rigorous, continuous-time treatment of default risk, when it was combined with the continuous-time hedging argument stemming from the Black-Scholes theory, led to the exact analysis of the event of default and of its consequences on derivative instruments. It could no longer rely on purely phenomenological measures such as the credit spread. Credit risk had to be modelled through a Poisson process triggering the default event, and the impact of the latter on the derivative instruments had to be made precise through the concept of recovery value.1 The intensity of the default Poisson process - also known as the hazard rate - became an integral part of the quantitative framework for pricing of convertible bonds. It would be implied from the traded prices of credit default swaps (CDSs) which, by now, had become fairly liquid.

Equity-to-credit

The problem enters into a new phase, however, and earns its emblematic appellation of 'equity-to-credit' once the event of default is expressed for the underlying equity itself. The modelling consensus in this regard is that the underlying share jumps to zero upon default. This has consequences on the valuation of all derivatives written on that underlying and not just the convertibles. Theoretically speaking, the model is no longer Black-Scholes, but turns into a jump-diffusion, which in many ways shocks the intuition and the experience of volatility traders trained in the Black-Scholes tradition.

Indeed, the jump to default - of magnitude -100% - creates massive skew for out-of-the-money puts as well as an upward-sloping implied volatility structure for at-the-money options. As a consequence, the volatility arbitrageur can no longer use the same implied volatility for the convertible bond as the equity option of similar strike and maturity. The default component has first to be extracted from the option premium, which of course reflects both Brownian volatility and the jump, and it is only the former that enters in the delta-hedging process to produce the desired bet on realised volatility.

How this is achieved is typically by inferring the hazard rate from the quoted spread of the CDS and by implying the 'remaining' Brownian volatility from the price of a reference equity option.

This Brownian volatility number comes out smaller, of course, than the Black-Scholes implied volatility that is referenced in the market as the option's conventional quote. Dynamic delta-hedging can then effectively play out implied Brownian volatility against the volatility that will be realised, provided the jump to default is independently hedged, for instance by a CDS.

The necessity of such dual hedging is not just specific to convertible bonds. Even the traditional volatility arbitrageurs, who would normally buy or sell equity options and rebalance their delta-hedge, must now do so in conjunction with a dynamic hedge involving the CDS. Option buyers who wish to trade realised volatility must, for instance, sell credit protection in a ratio that has to be computed by the model. The intuitive explanation is that the short sale of CDS finances the extra option premium that is generated by default risk and cannot otherwise be recovered by traditional delta-hedging under the (smaller) Brownian volatility. In the convertible bond's case, you sell credit protection to finance the extra credit premium inherent in the embedded equity option, and you buy credit protection to insure the bond component against default. Whether you end up long or short a net amount of credit protection will then depend on the recovery value of the convertible and the underlying stock level.

Not all equity options players are aware of this fundamental change that shakes their trading habits and breaks the integrity of their traditional trading, pricing and hedging system. To summarise, as soon as CDSs are traded and their spreads are observably substantial, credit risk can no longer be ignored. If, moreover, the default event is expected to trigger a sudden decline in the underlying share price, option premiums can no longer be explained and hedged with the traditional Black-Scholes model.

The arbitrageur must now deal with two separate underlyings (or state variables, or risk factors), the share price and the event of the default. Accordingly, two dynamic hedging ratios have to be computed, one applying to the share and the other to credit protection.

Two underlyings

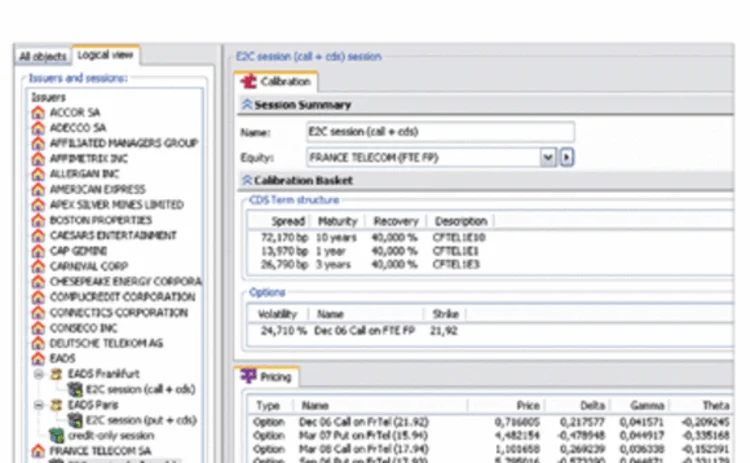
The duality of underlyings is the essence of the equity-to-credit paradigm. Not only does it impose on the volatility arbitrage desk to have access to the credit protection market, but it also entails a revision of the data model underlying its pricing and trading system. Simply put, the underlying equity can no longer be the originary node in a logical view such as that depicted in Figure 1. Convertible bonds, equity options and generally equity derivatives, are no longer derivative on the underlying equity alone because of their dramatic change in case of default. A more basic entity has to be found, which can underlie both the equity and the event of the default. This we have recognised to be the issuer.

CDSs, on the other hand, are not even written on the equity. For this reason they cannot be regrouped under its node. Yet they cannot be separated from it, because they are needed to infer the intensity of the Poisson process triggering its jump to default. This really points to another way in which the traditional data model and the traditional pricing logic have to be revised. Not only must the issuer replace the equity as primary node, but both the CDS and the equity option must now be subsumed under the same unit because they both serve to calibrate the one and same underlying process. Both an equity derivative and a credit derivative are needed to infer the two parameters of the equity-to-credit process, namely its Brownian volatility and hazard rate.

Under this new logic, we can no longer segregate between equity derivatives and equity volatility on one side, and credit derivatives and hazard rate on the other, as is still the case in the traditional architectures. Rather, a new entity called the 'session' is now recognised as the logical atom of calibration and pricing. Equity-to-credit is a hybrid process and, as such, it cannot relate to a single parameter or a single instrument. When all we had was the underlying equity, we could speak of its volatility as implied by the market price of an option or the market price of the convertible bond. With a slight abuse of language, we could talk of the 'implied volatility' of the option, or even of the convertible. This is no longer possible in the equity-to-credit paradigm, as we need to distinguish between Brownian volatility and hazard rate. A notion like the 'volatility of the convertible' becomes meaningless.

The session buffers any possible confusion. As session, it is neither purely equity nor purely credit, but imposes on the user that he completes the calibration of the hybrid process using both equity and credit derivatives, before he proceeds.

Note that the calibration of the equity-to-credit process can be achieved using nothing but equity derivatives. Out-of-the-money puts are frequently used as credit protection, and it is perfectly conceivable that both the Brownian volatility and the hazard rate should be inferred from the market price of an at-the-money option and an out-of-the-money put. Yet, for all that, the corresponding session will not be closed to CDSs, as they can be priced within it or even be used as dynamic credit hedge in the pricing of other instruments.

From the issuer's primary node, the logical view therefore branches immediately into the calibrated sessions. Sessions can be many under the same issuer, as they are distinguished by the nature of the derivative instruments they are calibrated against and the calibration results that may, accordingly, differ (see France Telecom in Figure 1). You should expect calibration to yield different values of the hazard rate depending on whether a CDS or an out-of-the-money put is used as credit reference. This is the key of the equity-to-credit arbitrage after all and the arbitrageur, when he is offered a chance to quantify the differences by visually comparing the two sessions, can now make up his mind on whether the CDS is too expensive or the out-of-the-money put too cheap.

Instruments in the equity-to-credit universe cannot be priced (or hedged) unless they are related to a session, which is in turn related to an issuer (see the France Telecom convertible in Figure 2). Indeed, only the session sets up the equity-to-credit parameters that are required for pricing and hedging. Reciprocally, you can limit yourself to a given session and price within it all the instruments relating to that issuer (see the pricing pane in Figure 1). The specific calibration basket of the calibrated session is visible at the top.

Exchangeable bonds

No case can give our logic a better check than the exchangeable bond. Exchangeable bond E is issued by issuer B and can be converted, or exchanged, into shares issued by a different entity A. As equity derivative, the exchangeable bond is underlain by the equity of issuer A, who may of course default. The corresponding equity-to-credit jump-diffusion process is calibrated in session(A) using, say, an option written on equity(A) and a CDS written on A. As credit derivative, the exchangeable bond bears the risk of signature of B and is therefore underlain by the event of default of B. The corresponding hazard rate is calibrated in session(B).

Note that the exchangeable bond E is not concerned with the Brownian volatility of equity(B), therefore session(B) appears as a pure credit session as far as E is concerned. Session(B) may otherwise be a full-blown equity-to-credit session, calibrated against both an option written on equity(B) and a CDS written on B for the sake of, for example, pricing a convertible bond issued by B. Yet, all that E really needs from session(B) is the hazard rate. As a matter of fact, issuer B may have issued no other bond than the exchangeable bond E, and he may even not have issued any equity at all.

So why bother with the calibration of the Brownian volatility of equity(B) in session(B) when all that that session is needed for is the pricing of E? This suggests that purely credit sessions should be conceivable after all, where the hazard rate is the only parameter and merely calibrated against the CDS.

There are cases, on the other hand, where issuers have multiple underlying equities. For instance, EADS has a share trading on the Euronext Paris exchange and a share trading on the Deutsche Borse. In such ambivalent cases, the next variable following the issuer's node in our logical view should be the equity, not the session which can only come second (Figure 1). When there is no ambiguity, however, sessions can still be attached directly to the issuer as previously indicated (France Telecom), the equity node here being implicit.

As for credit-only sessions, which are not concerned with equity and are solely used - in our system - to price a CDS or to take part in the pricing of an exchangeable bond, they are directly attached to the issuer, no matter what.

CONTACT

Elie Ayache, CEO

T: [phone]

E: [e-mail].

Sponsored content